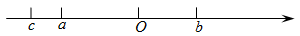2016年七年级下期数学入学考试选讲
可能您还没有从寒假的愉悦中缓过劲来,入学考试就来了,是的,初一下期的入学考试就这么来了,来了,来,了。。。。。。亲,您考的怎样?是否心情和下面的我一样?

已知\[A=2{{x}^{2}}+3xy-2x-y,B=-{{x}^{2}}+kxy-y\],若多项式\[3A+6B\]中不含$xy$项,则\[k\]的值为__________________. |
【来 源】《棕北中学七年级下入学考试》
【知识点】整式的加减—化简求值
【方法论】先化简,不含哪项,化简后哪项系数就为零
【难易度】☆☆☆
根据题意,先化简:
\[3A+6B=3(2{{x}^{2}}+3xy-2x-y)+6(-{{x}^{2}}+kxy-y)\]
\[=6{{x}^{2}}+9xy-6x-3y-6{{x}^{2}}+6kxy-6y\]
\[=(9+6k)xy-6x-9y\]
要不含xy项,则系数9+6k=0,解得\[k=-\frac{3}{2}\];
【攻略】此类问题一定要先化简,化简后得再看题目要求不含有的那项的系数,令系数为零,解出未知数即可。
有理数a,b,c在数轴上的位置如图所示,化简下式:|a-c|-|a-b|-|b-c|+|2a|,该式结果为___________________. |
【来 源】《棕北中学七年级下入学考试》
【知识点】数轴、绝对值
【方法论】首先判断每个绝对值符号内式子的正负性,再根据绝对值性质化简,最后合并同类项
【难易度】☆☆☆☆
依据数据上对应点的位置,容易得到c<a<0<b,进而可以得到:
| a-c>0,a-b<0,b-c>0,2a<0 | (判断绝对值内每个式子的正负性) |
| |a-c|-|a-b|-|b-c|+|2a|=(a-c)-[-(a-b)]-(b-c)+(-2a) | (化简绝对值) |
| =a-c+a-b-b+c-2a | (去括号) |
| =-2b | (合并同类项) |
【攻 略】绝对值的化简一直是初一小盆友的难点,但如果掌握好了绝对值的性质还是不难。此类题目关键有三点:1、准确判断绝对值内式子的正负性;2、化简的时候务必把括号加好,不要跳步骤;3、去括号的时候一定要仔细,学会检查。
关于x的方程kx+3=4x+1的解是正整数,则满足条件的所有整数k为_________________。 |
【来 源】《棕北中学七年级下入学考试》
【知识点】一元一次方程的解(含参数)
【方法论】说解就求解,含字母的用含字母的代数式表示出解
【难易度】☆☆☆☆
依据题意,首先尝试用含k的代数式表示x,易得:(k-4)x=-2
①若k-4=0,则0·x=2,无解,显然不合题意,此种情况不成立;
②若k-4≠0,则\[x=\frac{-2}{k-4}\],因为x为正整数,显然k-4应该是2的约数的相反数,即:k-4=-1或k-4=-2,解得k=2或k=3。
【攻略】此类题目有明显的特征,只要我们抓住特征,就有对应的解题方法。字母参数在这里并不可怕,我们可以把它当成未知数的系数,按照解一元一次方程的基本方法,把方程化简为ax=b的形式(特别说明,这里一般需要对a是否为零做分类讨论),在根据题意进行解答即可。
————————————————— 我是华丽丽的分割线 —————————————————
亲爱的同学们,您是否喜欢这样的讲解呢?如果喜欢,请点个赞,并在下面写出您的评论吧!如果您想看其他题目的讲解,也请您留言哦!
如果您是老师,那更请您点拨一二,也欢迎您加入到“得一”名师队伍当中来吧!
(得一小蜜蜂正在火热招募中,详情点击:首页>小蜜蜂招募贴)
-
-
 铃铛2016-02-29沙发回复
铃铛2016-02-29沙发回复 -
嗬嗬嗬2016-02-29板凳回复
-
hehe2016-02-29地板回复
-
清时明月2016-02-29地下室回复
-
高冷逗逼屌丝范儿2016-03-035 楼回复
-
高冷逗逼屌丝范儿2016-03-036 楼回复
-
高冷逗逼屌丝范儿2016-03-037 楼回复
-
高冷逗逼屌丝范儿2016-03-038 楼回复
-
高冷逗逼屌丝范儿2016-03-039 楼回复
-
高冷逗逼屌丝范儿2016-03-0310 楼回复
-
高冷逗逼屌丝范儿2016-03-0311 楼回复
-
高冷逗逼屌丝范儿2016-03-0312 楼回复
-
高冷逗逼屌丝范儿2016-03-0313 楼回复
-
高冷逗逼屌丝范儿2016-03-0314 楼回复
-
高冷逗逼屌丝范儿2016-03-0315 楼回复
 Ctrl+Enter 键快速提交回复
Ctrl+Enter 键快速提交回复 -
相关文章
-
1
74351
-
2
69802
-
3
40177
-
4
38164